鑫仔的个人站

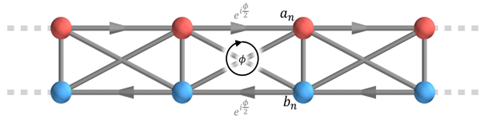
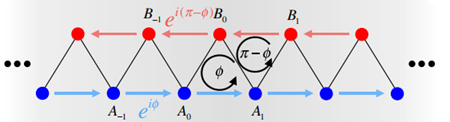
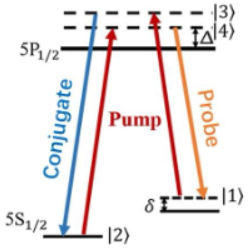
四波混频简介​ 四波混频过程是光与物质相互作用的非线性过程，是个三阶非线性过程，四个光波可以通过介质进行能量和动量的转移。 ​ 通常情况下，为两束不同频率的光在非线性介质中（例如光纤，非线性晶体，原子系综等）发生反应，并生成两束新的频率光束的效应。在这个过程中要满足能量守恒和相位匹配，像这样由四束不同频率的光参与的反应就被称为四波混频反应。 ​ 对于特殊的情况，存在一种简并形式的四波混频，当两束入射的pumb光是同一频率且共线传播时，在反应中一共存在三束频率的光。我们在Rb^{85}体系中我们所使用的就是这种特殊情况。 ​ 而在原子蒸汽中，强的非线性效应发生在光的频率接近原子能级共振区范围（近共振）。 Rb^{85}原子体系中的四波混频体系能级图​ Rb原子在该体系中的跃迁主要包含两个超精细能级结构的跃迁，即从基态5S_{\frac{1}{2}}跃迁到两个激发态5P_{\frac{1}{2}}和5P_{\frac{3}{2}}，这两个能级跃迁分别叫做铷原子的D1线和D2线如图1所示，由于波长在795nm的D1线的激发态5P_{\frac{1}{2}}的超精 ...

量子噪声​ 量子噪声是对于一个量子系统进行测量和控制过程中引入的不可避免的干扰和误差。 ​ 由广义不确定性原理，对于两个算符\hat{F}，\hat{G}，假设两个算符不可对易，且对易子满足[F,G]=ik，则有 。。。。。。。。 压缩光​ 压缩光作为一种非经典光源，是对光场某一正交分量量子噪声进行压缩，在不违背海森堡不确定性原理前提下，一个正交分量的不确定度大于标准量子极限，则另一个正交分量的不确定度将低于标准量子极限，也就是说压缩态光场能够用来突破标准量子极限(SQL)。 压缩态压缩算符​ 定义压缩算符为\hat{S}{(\xi)}=e^{\frac{1}{2}(\xi^*{\hat{a}}^2-\xi{\hat{a}}^{\dagger2})}，其中\xi=re^{i\theta}，r为压缩参数，\theta为压缩角。 ​ 可以看出\hat{S}中出现的是产生算符与压缩算符的二次方，由此可以推断压缩算符可能会与一些双光子的过程有关。同时可以看出压缩算符是幺正的，这也意味着我们可以适当的设计一个哈密顿量，让其成为一个时间演化算符，使系统演化成相应的压 ...

半经典理论：光场用Maxwell方程描述，原子或电子遵循薛定谔方程，适用领域：光场的量子涨落效应不太显著。 单模光场与原子相互作用的半经典理论​ 对于单模光场与多能级原子的相互作用，我们首先列出该原子的薛定谔方程 系统哈密顿量​ 该系统的哈密顿量可以表示为：H=H_A+H'，其中H_A为原子自由哈密顿量，通常采用原子的自身表象，H'为相互作用哈密顿量。 ​ 此时对于H_A,其本征值方程为:H_A\mid{k}>=E_k\mid{k}>=\hbar\omega_k\mid{k}>，此时采用原子自身表象，H_A可以表示为H_A=\sum_k(\hbar\omega_k\mid{k}>与\mid{g}>为基矢的表象中可写为:H=\hbar\omega_g\mid{g}>

纯态和混态纯态(pure state)​ 可以用态矢量描述的量子态即为纯态\mid\varphi>。 混态(mixed state)​ 混态本质上是一种统计系综，是大量性质相同各自独立的系统的集合。在这些系统当中，我们知道有多少系统处于不同的量子态 中。此时我们在这些系统中拿出一个系统来，我们想描述这个系统的状态，但我们无法确定这个系统到底处于哪个状态上，而是我们能说他是以不同的概率p_n处于\mid\varphi_n>上。 密度算符(density operator)表示 对于纯态$$\mid\varphi>$$，密度算符可以表示为：$$\rho=\mid\varphi><\varphi\mid$$ ​ 对于混态，我们需要将其中的每一个参与态做外积，乘以相应的几率，然后对所有可能的参与态进行求和\rho=\sum_n{p_n}\mid\varphi_n>，不要求其满足正交完备性。 ​ 再者，在混态的密度算符中，对于同一个\rho，他们参与态的形式并不唯一。并且其可能的参与态方式是有无穷多个，在所有这些不同的参与方式中，里面一定存在一组正交归一 ...

饱和吸收谱一般在实验上用于找对照点，之后详述。 饱和吸收谱简介​ 饱和吸收光谱(saturated absorption spectroscopy)是一种测量原子吸收光谱的技术，其不会被由原子热运动的引入的多普勒频移影响，运用饱和吸收谱，我们可以找出原子能级跃迁的真实谱线。 原理光谱原理​ 原子核周围的电子有一些不同的能级，当有一束光打到这个原子上的时候，如果这个光的频率正好满足电子的跃迁频率，电子就会吸收光子并在能级间跃迁，比如从基态跃迁到激发态，也就是发生了泵浦。而当电子从激发态再回到基态的时候，相应的就会发出一个光子，也就是弛豫。我们可以通过给原子不同频率的光，通过观察透射谱看它对于光的吸收与发射情况，以此得到一些信息，这就是光谱的基本的原理。 光谱展宽​ 从刚才的光谱原理我们知道，电子从激发态降到基态，放出一个确定的频率光，按理说它光谱应该是一条在该频率处的直线，但是实际上，它并不是直线，而是一个在跃迁频率附近有一定线宽的图形，如图1所示。 图1 原子自发辐射产生的光谱 ​ 这是因为光谱发生了展宽，造成展宽的因素主要有三个： 自然展宽：由量子力学的 ...

立个坑，记录下EIT的完整推导过程 电磁诱导透明（EIT）EIT简介​ 电磁诱导透明(EIT)即”electromagnetically induced transparency”，是在三能级原子组成的一个介质中，在强驱动电磁场的作用下对弱探测电磁场呈现透明的现象。 ​ 所谓透明的现象就是指的是这个体系对弱探测电磁场是没有作用的，包括：吸收和相互之间的一些作用，因此我们无法观测到他，则他是透明的。 ​ 电磁诱导透明是一般是用两束光同时照射到原子介质，使得其中一束光能够在与原子跃迁共振时通过原子介质而不产生吸收和反射的现象。如图1所示 ​ EIT是一种典型的量子相干效应，其本质为强耦合光影响了吸收介质的色散性质，从而使介质对弱探测光的吸收减小甚至完全透明。 图1 能级示意图 EIT推导系统哈密顿量​ 在薛定谔绘景下，体系哈密顿量包含两部分：H=H_0+V， ​ 其中H_0是自由哈密顿量部分，即H_0=\hbar\omega_a\mid{a}>

之前有个任务，将实验上所记录的数据修改为所需要的里德堡双稳态图，有时间的话我记录下代码

所述论文Flat-Band Localization in Creutz Superradiance Lattices 背景紧束缚晶格：​ 具有平移对称性的系统在物理学中很常见，例如晶体中原子的周期性排列，当所有相邻位置的波函数的重叠很小以至于可以忽略时，波函数被认为在其晶格位置周围很好地局部化了，这便是紧束缚近似。 ​ 在这种近似中，波函数存在于空间中的离散点中，因此可以通过其晶格位置的索引来标记，其传输仅通过相邻格点的hopping发生。 平带：​ 平带是无色散的能带，其的一大特征是粒子的群速度为0，同时，由于平带上粒子有效质量很大，相比于动能整个系统会对一些特殊的势能非常敏感，这使得平带被认为是研究多体现象的理想体系。 ​ 对于平带的最简单构造，我们可以从孤立格点的情况考虑，当所有跳变都为0时，系统的单粒子定态薛定谔方程如下所示： H\mid\psi>=E\mid\psi>\tag{1}​ 我们将整体的波函数用单个晶胞的波函数作为基展开，带入薛定谔方程中得到此时的特征值问题如下公式: \varepsilon_{j}\phi_{nj}=E\phi_{n ...

所述论文Experimental Observation of Momentum-Space Chiral Edge Currents in Room-Temperature Atoms 背景量子霍尔效应​ 霍尔效应的示意图如图1，当电流垂直于外磁场通过导体或半导体时，在垂直于磁场和电流方向会出现一个稳定的电势差，其原理是因为洛伦兹力与电场力平衡。 图1 霍尔效应示意图 ​ 然而，我们之后发现其存在量子版本，在极低温和强磁场下，对于二维体系的霍尔效应实验中，我们发现其霍尔电阻并不随着磁场强度增大做线性变化，而是呈分立排布，这就是量子霍尔效应。 图2 量子霍尔效应示意图 之后补充 手性边缘流 图3 手性边缘流示意图 超辐射晶格​ 超辐射晶格的实验手段是通过驻波耦合的EIT，以此在动量空间中构建出具有不同动量的超辐射态。由于在超辐射晶格中，原子运动所引入的多普勒频移对应晶格中的有效电场，因此常可用于室温原子中进行量子模拟 图4 驻波耦合EIT示意图 ​ 超辐射晶格在动量空间示意图如图所示，其格点是一个个不同动量的TDS态，我们通过弱probe ...

Welcome to Hexo! This is your very first post. Check documentation for more info. If you get any problems when using Hexo, you can find the answer in troubleshooting or you can ask me on GitHub. Quick StartCreate a new post1$ hexo new "My New Post" More info: Writing Run server1$ hexo server More info: Server Generate static files1$ hexo generate More info: Generating Deploy to remote sites1$ hexo deploy More info: Deployment