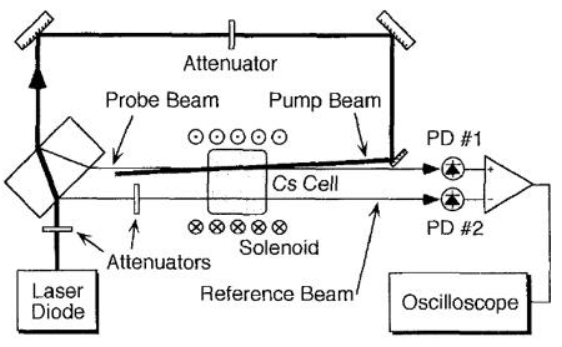
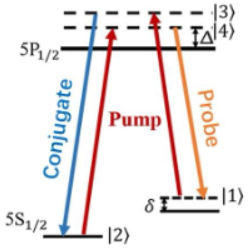
单模光与多能级原子相互作用的半经典理论

半经典理论：光场用Maxwell方程描述，原子或电子遵循薛定谔方程，适用领域：光场的量子涨落效应不太显著。

单模光场与原子相互作用的半经典理论

​ 对于单模光场与多能级原子的相互作用，我们首先列出该原子的薛定谔方程

系统哈密顿量

​ 该系统的哈密顿量可以表示为：$H=H_A+H'$，其中$H_A$为原子自由哈密顿量，通常采用原子的自身表象，$H'$为相互作用哈密顿量。

​ 此时对于$H_A$,其本征值方程为:$H_A\mid{k}>=E_k\mid{k}>=\hbar\omega_k\mid{k}>$，此时采用原子自身表象，$H_A$可以表示为$H_A=\sum_k(\hbar\omega_k\mid{k}><k\mid)$。

​ 考虑光场与原子的相互作用。光场是一种电磁场，既存在电场也存在磁场，他们均会与原子发生相互作用，可是在通常情况下，电场与原子发生相互作用的强度相比磁场而言大很多（大两个数量级）。此时，我们可以忽略磁场，在考虑光与物质的相互作用时通常只考虑电磁波的电场，而不考虑其磁场。同时，在半经典理论中，我们将电场按照经典场来处理，即$\textbf{E}=\vec{e}{\xi}cos(\omega_Lt-\textbf{k}\cdot\textbf{r}+\phi)$。其中$\vec{e}$为电场偏振方向，$\omega_L$为电场频率。

​ 再考虑光与原子相互作用中，电偶极相互作用是最强的，采用电偶极近似，则光与原子相互作用的哈密顿量为：$H_1=-\hat{d}{\cdot}E$。其中$\hat{d}$是原子的电偶极矩算符：$\hat{d}=-e\textbf{r}$。此时在$H_A$表象中：$\hat{d}=\sum_j\mid{j}><j\mid\hat{d}\sum_k\mid{k}><k\mid=\sum_{j,k}\vec{d}_{jk}\mid{j}><k\mid$。其中$\vec{d}_{jk}=<j\mid{\vec{d}}\mid{k}>$为电偶极矩矩阵元

​ 由此我们得到单模光场与原子相互作用的半经典哈密顿量：$H=\sum_k(\hbar\omega_k\mid{k}><k\mid)-\sum_{j,k}\vec{E}\cdot\vec{d}_{jk}\mid{j}><k\mid$。此时哈密顿量中并没有光场所代表的算符，因此我们实际上在半经典理论中是将光场作为环境来处理的(这一点日后要同缀饰态区分)。

​ 最后，对于光场$\textbf{E}=\hat{e}{\xi}cos(\omega_Lt-\textbf{k}\cdot\textbf{r}+\phi)$，由于原子线度约为$10^{-10}m$，而可见光与微波波段$\lambda\approx400-700nm$，因此在原子范围内我们可以将光场看成是均匀的，此时可以取原子当地电场值来进行计算，而忽略其随空间的变化，这称为长波近似。取原子位置为坐标原点（r=0)，于是电场为$\textbf{E}=\vec{e}{\xi}cos(\omega_Lt+\phi)$。

单模光场与二能级系统的相互作用

系统哈密顿量

​ 对于二能级系统，由上节可知，系统的哈密顿量在以$\mid{e}>$与$\mid{g}>$为基矢的表象中可写为:$H=\hbar\omega_g\mid{g}><g\mid+\hbar\omega_e\mid{e}><e\mid-\vec{E}(\vec{d}_{eg}\mid{e}><g\mid+\vec{d}_{ge}\mid{g}><e\mid)$。其中$d_{eg}$和$d_{ge}$分别为对应的偶极跃迁矩阵元，在二能级系统中相等。

​ 同时为简化起见，定义拉比频率$\Omega_R$：$\Omega_R=\frac{-d_{eg}{\xi}}{\hbar}=\frac{er_{eg}{\xi}}{\hbar}$。

​ 则系统哈密顿量可写为：$H=H_A+H'=\hbar\begin{pmatrix}\omega_e & \Omega_Rcos(\omega_Lt+\phi) \\ \Omega_Rcos(\omega_Lt+\phi) & \omega_g \end{pmatrix}$

​ 我们可以整体移动能量零点来使得哈密顿量更方便求解，令$\omega_e=-\omega_g=\frac{1}{2}(\omega_e-\omega_g)=\frac{1}{2}\omega_0$，

​ 此时：$H=\hbar\begin{pmatrix}\frac{1}{2}\omega_0 & \Omega_Rcos(\omega_Lt+\phi) \\\Omega_Rcos(\omega_Lt+\phi) &- \frac{1}{2}\omega_0\end{pmatrix}$

​ 也可以用泡利矩阵的形式写为：$H=\frac{1}{2}\hbar\omega_0\sigma_z+\hbar\Omega_R(\sigma^++\sigma^-)cos(\omega_Lt+\phi)$。

系统薛定谔方程的求解

​ 我们通过求解二体系统中的薛定谔方程，以得到波函数在该系统中的演化过程。

​ 在基矢$\mid{e}>$和$\mid{g}>$所张成的空间中，原子的波函数可以写为：$\mid\varphi>=C_e(t)\mid{e}>+C_g(t)\mid{g}>$。定义$\begin{cases}c_e=C_ee^{i\omega_0t/2}\\c_g=C_ge^{-i\omega_0t/2}\end{cases}$，将其带入二能级系统的薛定谔方程，解之得：$\begin{cases}\dot{c}_e=-i\frac{\Omega_R}{2}c_g[e^{i(\omega_0-\omega_L)t-i\phi}+e^{i(\omega_0+\omega_L)t+i\phi}]\\\dot{c}_g=-i\frac{\Omega_R}{2}c_e[e^{-i(\omega_0-\omega_L)t+i\phi}+e^{-i(\omega_0+\omega_L)t-i\phi}]\end{cases}$