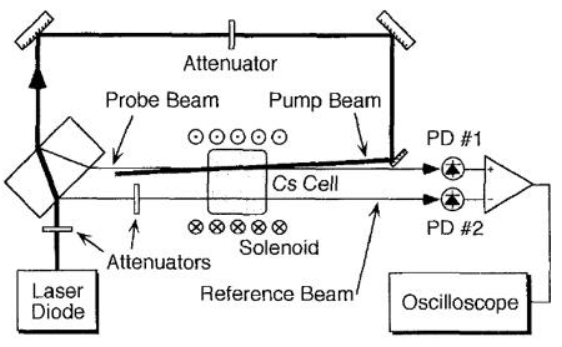
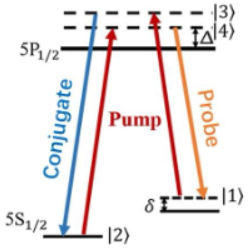
压缩光

量子噪声

​ 量子噪声是对于一个量子系统进行测量和控制过程中引入的不可避免的干扰和误差。

​ 由广义不确定性原理，对于两个算符$\hat{F}$，$\hat{G}$，假设两个算符不可对易，且对易子满足$[F,G]=ik$，则有

。。。。。。。。

压缩光

​ 压缩光作为一种非经典光源，是对光场某一正交分量量子噪声进行压缩，在不违背海森堡不确定性原理前提下，一个正交分量的不确定度大于标准量子极限，则另一个正交分量的不确定度将低于标准量子极限，也就是说压缩态光场能够用来突破标准量子极限(SQL)。

压缩态

压缩算符

​ 定义压缩算符为$\hat{S}{(\xi)}=e^{\frac{1}{2}(\xi^*{\hat{a}}^2-\xi{\hat{a}}^{\dagger2})}$，其中$\xi=re^{i\theta}$，$r$为压缩参数，$\theta$为压缩角。

​ 可以看出$\hat{S}$中出现的是产生算符与压缩算符的二次方，由此可以推断压缩算符可能会与一些双光子的过程有关。同时可以看出压缩算符是幺正的，这也意味着我们可以适当的设计一个哈密顿量，让其成为一个时间演化算符，使系统演化成相应的压缩态，这一点从后面我们可以看出。

​ 由B-H恒等式可以推算出：$\hat{S}^\dagger\hat{a}\hat{S}=\hat{a}coshr-{\hat{a}^\dagger}e^{i\theta}sinhr$

压缩真空态

​ 特别的，考虑当压缩算符作用在真空态上时，将得到压缩真空态，记为：$\mid\xi>=\hat{s}{(\xi)}\mid0>$。

---

​ 对于压缩真空态的基本性质，有以下几点：

1. 在压缩真空态下粒子数N的平均值为：$<N>=<\xi\mid{a^{\dagger}a}\mid\xi>=<0\mid{S^\dagger{a^\dagger{aS}}}\mid0>=sinh^2r$，

   同时$N^2$的平均值为：$<N^2>=<\xi\mid{(a^{\dagger}a)^2}\mid\xi>=2sinh^2rcosh^2r+sinh^2r$，

   由此我们可以计算出粒子数的涨落（方差）为：$V(N)=<N^2>-<N>^2=2sinh^2rcosh^2r=2<N>(<N>+1)$。

   经过计算可知其粒子数分布是超泊松分布。

2. 在压缩真空态下$<a>=0$

3. 对于系统的两个正交分量$X_1,X_2$（$\hat{X}_1=\frac{\hat{a}+\hat{a}^\dagger}{2},\hat{X}_2=\frac{\hat{a}-\hat{a}^\dagger}{2i}$）有其平均值为0（$<X_1>=<X_2>=0$）。

   经过计算最终得到其方差为：$(\triangle\hat{X}_{12})^2=\frac{cosh^2r+sinh^2r\mp{2sinhrcoshrcos\theta}}{4}$。

   由此我们得到，当$\theta=0$时，$(\triangle{\hat{X}_1})^2=\frac{e^{-2r}}{4}，(\triangle{\hat{X}_2})^2=\frac{e^{2r}}{4}$，此时二者的乘积仍然为$\frac{1}{4}$，因此压缩真空态仍然为最小不确定度态，但是在正交分量$X_1$处的涨落被压缩得更小了，以此为代价的是在$X_2$方向上的涨落被放大了。

   而当$\theta=\pi$时，$\triangle{\hat{X}_1}=\frac{e^{2r}}{4}，\triangle{\hat{X}_2}=\frac{e^{-2r}}{4}$，同理可以看出，此时的压缩真空态也为最小不确定度态，并且也被压缩了，只是压缩方向变为了$X_2$方向，由此我们可以得到，$\theta$影响着压缩方向。

---

​ 为了赋予$\theta$几何意义，考虑到当$\theta$从0变化到$\pi$时，旋转方向可看作旋转了$\frac{\pi}{2}$。因此不妨考虑将$X_1,X_2$旋转$\frac{\pi}{2}$形成新算符$Y_1,Y_2$。

​ 有$\begin{pmatrix}\hat{Y}_1 \\ \hat{Y}_2 \end{pmatrix}=\begin{pmatrix}cos\frac{\theta}{2}&sin\frac{\theta}{2}\\-sin\frac{\theta}{2}&cos\frac{\theta}{2} \end{pmatrix}\begin{pmatrix}\hat{X}_1\\\hat{X}_2 \end{pmatrix}$

​ 此时我们可以解出$\begin{cases} \hat{Y}_1=\frac{1}{2}(ae^{-i\theta/2}+a^\dagger{e^{i\theta/2}}) \\\hat{Y}_2=\frac{1}{2i}(ae^{-i\theta/2}-a^\dagger{e^{i\theta/2}})\end{cases}$

​ 由此可以得到$(\triangle{\hat{Y}_1})^2=\frac{e^{-2r}}{4}，(\triangle{\hat{Y}_2})^2=\frac{e^{2r}}{4}$，此时我们可以将$Y_1,Y_2$视作压缩态的两个长短轴

压缩态表示

​ 由于我们的相干态可以用平移算符产生：$\mid{\alpha}>=\hat{D}(\alpha)\mid{0}>$，其中$\hat{D}(\alpha)=e^{\alpha\hat{a}^\dagger-\alpha^*\hat{a}}$由此，我们可以将平移算符作用在压缩真空态上得到更加一般的压缩态的表示形式：$\mid{\alpha,\xi}>=\hat{D}(\alpha)\hat{S}(\xi)\mid{0}>$

​ 此时压缩态会在$Y_1,Y_2$坐标轴上存在平移……